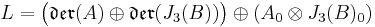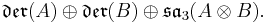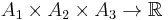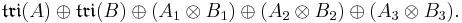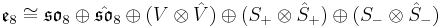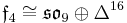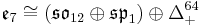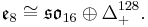Freudenthal magic square
In mathematics, the Freudenthal magic square (or Freudenthal–Tits magic square) is a construction relating several Lie groups. It is named after Hans Freudenthal and Jacques Tits, who developed the idea independently. It associates a Lie group (or corresponding Lie algebra) to a pair of division algebras A, B. The resulting Lie algebras have Dynkin diagrams according to the following table.
| A \ B | R | C | H | O |
|---|---|---|---|---|
| R | A1 | A2 | C3 | F4 |
| C | A2 | A2 × A2 | A5 | E6 |
| H | C3 | A5 | D6 | E7 |
| O | F4 | E6 | E7 | E8 |
The Freudenthal magic square includes all of the exceptional Lie groups apart from G2, and it provides one possible approach to justify the assertion that "the exceptional Lie groups all exist because of the octonions": G2 itself is the automorphism group of the octonions (also, it is in many ways like a classical Lie group because it is the stabilizer of a generic 3-form on a 7-dimensional vector space – see prehomogeneous vector space).
Contents |
Constructions
Tits' approach
Associated with any normed real division algebra A (i.e., R, C, H or O) there is a Jordan algebra
- J3(A)
of 3×3 A-Hermitian matrices. For any pair
- (A,B)
of such division algebras, one can define a Lie algebra
where der denotes the Lie algebra of derivations of an algebra, and the subscript 0 denotes the trace-free part. The Lie algebra L has 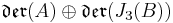 as a subalgebra, and this acts naturally on
as a subalgebra, and this acts naturally on 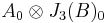 . The Lie bracket on
. The Lie bracket on 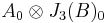 (which is not a subalgebra) is not obvious, but Tits showed how it could be defined, and that it produced the following table of compact Lie algebras.
(which is not a subalgebra) is not obvious, but Tits showed how it could be defined, and that it produced the following table of compact Lie algebras.
| B | R | C | H | O | |
|---|---|---|---|---|---|
| A | der(A/B) | 0 | 0 | 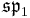 |
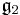 |
| R | 0 | 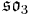 |
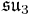 |
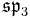 |
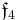 |
| C | 0 | 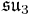 |
 |
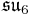 |
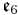 |
| H | 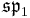 |
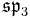 |
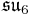 |
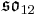 |
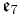 |
| O | 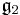 |
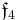 |
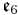 |
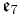 |
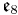 |
Note that by construction, the row of the table with A=R gives der(J3(B)), and similarly vice versa.
Vinberg's symmetric method
The "magic" of the Freudenthal magic square is that the constructed Lie algebra is symmetric in A and B. This is not obvious from Tits' construction. Ernest Vinberg gave a construction which is manifestly symmetric. Instead of using a Jordan algebra, he uses an algebra of skew-hermitian trace-free matrices with entries in 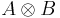 , denoted
, denoted 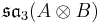 . Vinberg defines a Lie algebra structure on
. Vinberg defines a Lie algebra structure on
When A and B have no derivations (i.e., R or C), this is just the Lie (commutator) bracket on 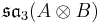 . In the presence of derivations, these form a subalgebra acting naturally on
. In the presence of derivations, these form a subalgebra acting naturally on 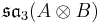 as in Tits' construction, and the tracefree commutator bracket on
as in Tits' construction, and the tracefree commutator bracket on 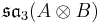 is modified by an expression with values in
is modified by an expression with values in  .
.
Triality
A more recent construction, suggested by Pierre Ramond and developed by Chris Barton and Anthony Sudbery, uses triality in the form developed by John Frank Adams. Whereas Vinberg's construction is based on the automorphism groups of a division algebra A (or rather their Lie algebras of derivations), Barton and Sudbery use the group of automorphisms of the corresponding triality. The triality is the trilinear map
obtained by taking three copies of the division algebra A, and using the inner product on A to dualize the multiplication. The automorphism group is the subgroup of SO(A1)×SO(A2)×SO(A3) preserving this trilinear map. It is denoted Tri(A). The following table compares its Lie algebra to the Lie algebra of derivations.
| A: | R | C | H | O |
|---|---|---|---|---|
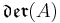 |
0 | 0 | 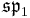 |
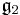 |
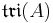 |
0 |  |
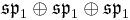 |
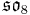 |
Barton and Sudbery then identify the magic square Lie algebra corresponding to (A,B) with a Lie algebra structure on the vector space
The Lie bracket is compatible with a Z2×Z2 grading, with tri(A) and tri(B) in degree (0,0), and the three copies of 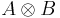 in degrees (0,1), (1,0) and (1,1). The bracket preserves tri(A) and tri(B) and these act naturally on the three copies of
in degrees (0,1), (1,0) and (1,1). The bracket preserves tri(A) and tri(B) and these act naturally on the three copies of 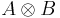 , as in the other constructions, but the brackets between these three copies are more constrained.
, as in the other constructions, but the brackets between these three copies are more constrained.
For instance when A and B are the octonions, the triality is that of Spin(8), the double cover of SO8, and the Barton-Sudbery description yields
where V, S+ and S- are the three 8 dimensional representations of 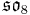 (the fundamental representation and the two spin representations), and the hatted objects are an isomorphic copy.
(the fundamental representation and the two spin representations), and the hatted objects are an isomorphic copy.
With respect to one of the Z2 gradings, the first three summands combine to give 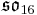 and the last two together form one of its spin representations Δ+128 (the superscript denotes the dimension). This is a well known symmetric decomposition of E8.
and the last two together form one of its spin representations Δ+128 (the superscript denotes the dimension). This is a well known symmetric decomposition of E8.
The Barton-Sudbery construction extends this to the other Lie algebras in the magic square. In particular, for the exceptional Lie algebras in the last row (or column), the symmetric decompositions are:
Generalizations
Split composition algebras
In addition to the normed division algebras, there are other composition algebras over R, namely the split-complex numbers, the split-quaternions and the split-octonions. If one uses these instead of the complex numbers, quaternions, and octonions, one obtains the following variant of the magic square (where the split versions of the division algebras are denoted by a dash).
| A\B | R | C' | H' | O' |
|---|---|---|---|---|
| R | 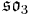 |
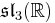 |
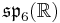 |
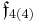 |
| C' | 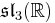 |
 |
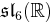 |
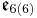 |
| H' | 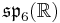 |
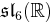 |
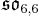 |
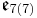 |
| O' | 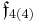 |
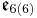 |
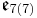 |
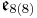 |
Here all the Lie algebras are the split real form except for so3, but a sign change in the definition of the Lie bracket can be used to produce the split form so2,1. In particular, for the exceptional Lie algebras, the maximal compact subalgebras are as follows:
| Split form | 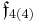 |
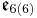 |
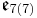 |
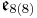 |
|---|---|---|---|---|
| Maximal compact |  |
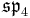 |
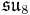 |
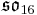 |
A non-symmetric version of the magic square can also be obtained by combining the split algebras with the usual division algebras. According to Barton and Sudbery, the resulting table of Lie algebras is as follows.
| A\B | R | C | H | O |
|---|---|---|---|---|
| R | 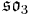 |
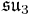 |
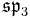 |
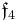 |
| C' | 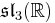 |
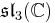 |
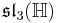 |
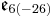 |
| H' | 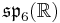 |
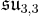 |
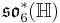 |
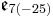 |
| O' | 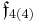 |
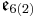 |
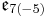 |
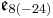 |
The real exceptional Lie algebras appearing here can again be described by their maximal compact subalgebras.
| Lie algebra | 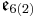 |
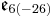 |
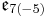 |
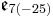 |
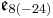 |
|---|---|---|---|---|---|
| Maximal compact |  |
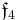 |
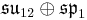 |
 |
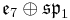 |
Arbitrary fields
The split forms of the composition algebras and Lie algebras can be defined over any field K. This yields the following magic square.
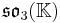 |
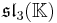 |
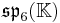 |
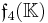 |
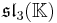 |
 |
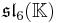 |
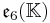 |
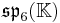 |
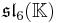 |
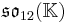 |
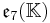 |
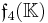 |
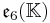 |
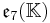 |
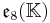 |
There is some ambiguity here if K is not algebraically closed. In the case K=C, this is the complexification of the Freudenthal magic squares for R discussed so far.
More general Jordan algebras
The squares discussed so far are related to the Jordan algebras J3(A), where A is a division algebra. There are also Jordan algebras Jn(A), for any positive integer n, as long as A is associative. These yield split forms (over any field K) and compact forms (over R) of generalized magic squares.
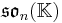 |
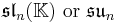 |
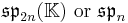 |
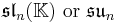 |
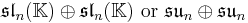 |
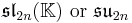 |
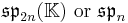 |
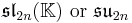 |
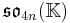 |
For n=2, J2(O) is also a Jordan algebra. In the compact case (over R) this yields a magic square of orthogonal Lie algebras.
| A\B | R | C | H | O |
|---|---|---|---|---|
| R | 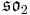 |
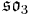 |
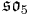 |
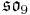 |
| C | 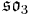 |
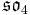 |
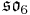 |
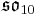 |
| H | 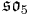 |
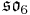 |
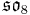 |
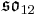 |
| O | 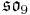 |
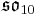 |
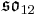 |
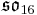 |
The last row and column here are the orthogonal algebra part of the isotropy algebra in the symmetric decomposition of the exceptional Lie algebras mentioned previously.
These constructions are closely related to hermitian symmetric spaces – cf. prehomogeneous vector spaces.
See also
- E8 (mathematics)
- E7 (mathematics)
- E6 (mathematics)
- F4 (mathematics)
- G2 (mathematics)
- Jordan triple system
References
- John Frank Adams (1996), Lectures on Exceptional Lie Groups (Chicago Lectures in Mathematics), edited by Zafer Mahmud and Mamora Mimura, University of Chicago Press, ISBN 0-226-00527-5.
- Baez, John (2002), "The Octonions, §4.3: The Magic Square", Bulletin of the American Mathematical Society 39: 145–205, ISSN 0273-0979, http://www.ams.org/bull/2002-39-02/S0273-0979-01-00934-X/home.html; also available here, arXiv:math.AG/0105155.
- C. H. Barton and A. Sudbery (2003), Magic squares and matrix models of Lie algebras, Adv. in Math. 180 (2003), 596-647, arXiv:math.RA/0203010.
- J.M. Landsberg and L. Manivel (2001), The projective geometry of Freudenthal's magic square, Journal of Algebra, Volume 239, Issue 2, pages 477-512, doi:10.1006/jabr.2000.8697, arXiv:math.AG/9908039.
- Pierre Ramond (1976), Introduction to Exceptional Lie Groups and Algebras, CALT-68-577, California Institute of Technology, Pasadena.